++ 50 ++ 平行四辺形 対角線 ���さ 違う 220933-平行四辺形 対角線 長さ 違う

小学校5年生の算数 三角形の面積計算 をやってみた 赤髪デザイナーmoekoosawaカラフルdays

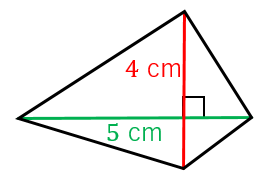
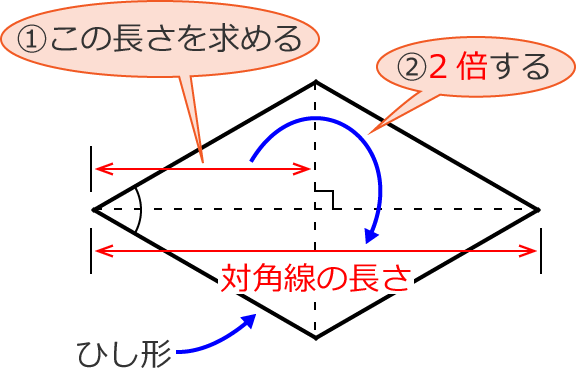
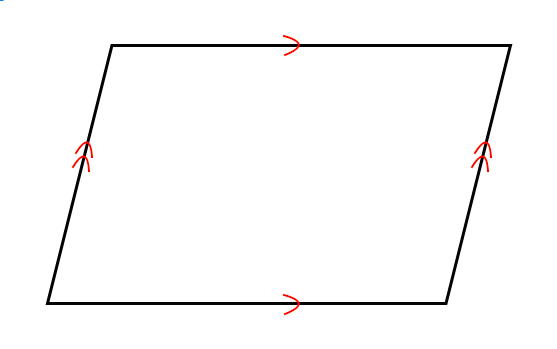
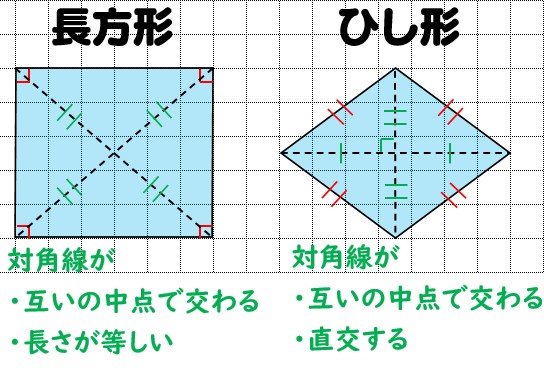
 平行四辺形の定義↓ 2組の対辺がそれぞれ等しい。 2組の対角がそれぞれ等しい。 2組の対辺がそれぞれ平行。 2本の対角線がともに、互いの中点で交わる。 1組の対辺が平行であり、かつその長さが等しい。 です！ サウラ 2年以上前 平行四辺形は2組の対辺の長さがそれぞれ等しいという性質をもっています！ yuka 2年以上前 ありがとうございます^^* サウラ 2年以上前ひし形の面積は 2 2 つの対角線の長さをかけて2で割ったもの、つまり 『対角線×対角線÷2 ÷ 2 』 で求めることができます。 平行四辺形の一種でもあるので、底辺と高さが分かっていれば『底辺×高さ』でも求められます。 たとえば以下のような問題の場合

平行四辺形 対角線 長さ 違う

平行四辺形 対角線 長さ 違う- 同じく平行四辺形から 1．1 つの角を直角にする。 2．対角線の長さを等しくする。 のどちらかをすると長方形になります。 長方形もひし形も平行四辺形の特殊な形ですからね 長方形の対角線は等しいというか 対角線を等しくすると長方形になる って方 始点の揃った 2 つのベクトルで平行四辺形を描き、その平行四辺形の対角線の方向と長さ です。 言葉だと難しいので図に表します。

教えてください Clearnote

今回はその2つ目の性質の 対角の角度が等しい こと確認していきましょう。 もし、平行四辺形の残り2つの性質についても詳しく知りたい場合は、下のリンクに説明を書いているので、参考にしてみて下さいね。 "平行四辺形の対辺の長さは等しくなる"ことの説明 2組の対辺がそれぞれ平行な四角形を、平行四辺形と定義されます。 平行四辺形は対辺が平行になっ6「平行線の同位角と錯角・円周角の性質・平行四辺形の性質」 1 出題の趣旨 平行線の性質を用いて，角の大きさを求めることができるかどうかをみる。 円周角の性質を用いて，角の大きさを求めることができるかどうかをみる。平行四辺形において 1．対角線の長さが等しいなら長方形である 正方形の対角線 正方形の対角線の長さの求め方には、公式があります。 対角線の長さ＝√2×（1辺の長さ） となります。 よって下図のような正方形においては、対角線BDの長さXは、√2aです。 なぜこのような公式が導かれるかといえば、対角線と正方形の2辺で作られる直角三角形で三平方の定理を使っているだけです。 下図の正方形なら、 ABDにおいて

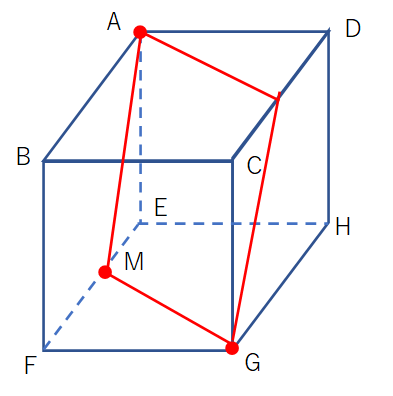
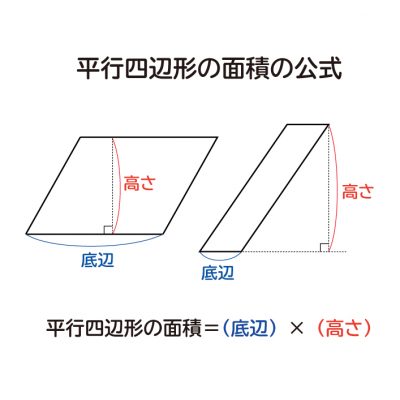
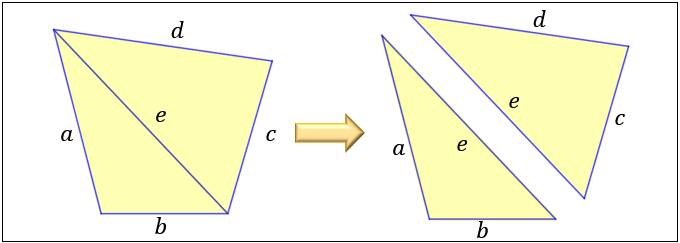
 ミズキ こんにちは、ミズキです。 ミズキ 今回は様々な四角形について、一緒に考えていきましょう。 カイト よろしくな！ ミズキ！ ミズキ アオイくんにも、手伝ってもらいます。 アオイ カイにも分かるように、頑張って教えよう。 ミズキ さて、それでは、まず平行四辺形の面積の公式にC27 平行四辺形は，対角線が垂直で交わってび方， 青新しい知識、 赤情 いない。対角線の長さも違う。対角線の意が書かれていることが分 長さと交わり方を調べれば図形の名前がかるように三色ペンで視覚 分かる。 的にラインを引き返却する。 （3）本時の評価 対角線の意味を理解し，その三角形は面積が等しくなります （2）は 「等積変形」を 利用すると とても簡単で

平行四辺形 対角線 長さ 違うのギャラリー

各画像をクリックすると、ダウンロードまたは拡大表示できます

平行四辺形であることを証明する 苦手な数学を簡単に	平行四辺形であることを証明する 苦手な数学を簡単に	平行四辺形であることを証明する 苦手な数学を簡単に
平行四辺形であることを証明する 苦手な数学を簡単に	平行四辺形であることを証明する 苦手な数学を簡単に	平行四辺形であることを証明する 苦手な数学を簡単に
平行四辺形であることを証明する 苦手な数学を簡単に	平行四辺形であることを証明する 苦手な数学を簡単に	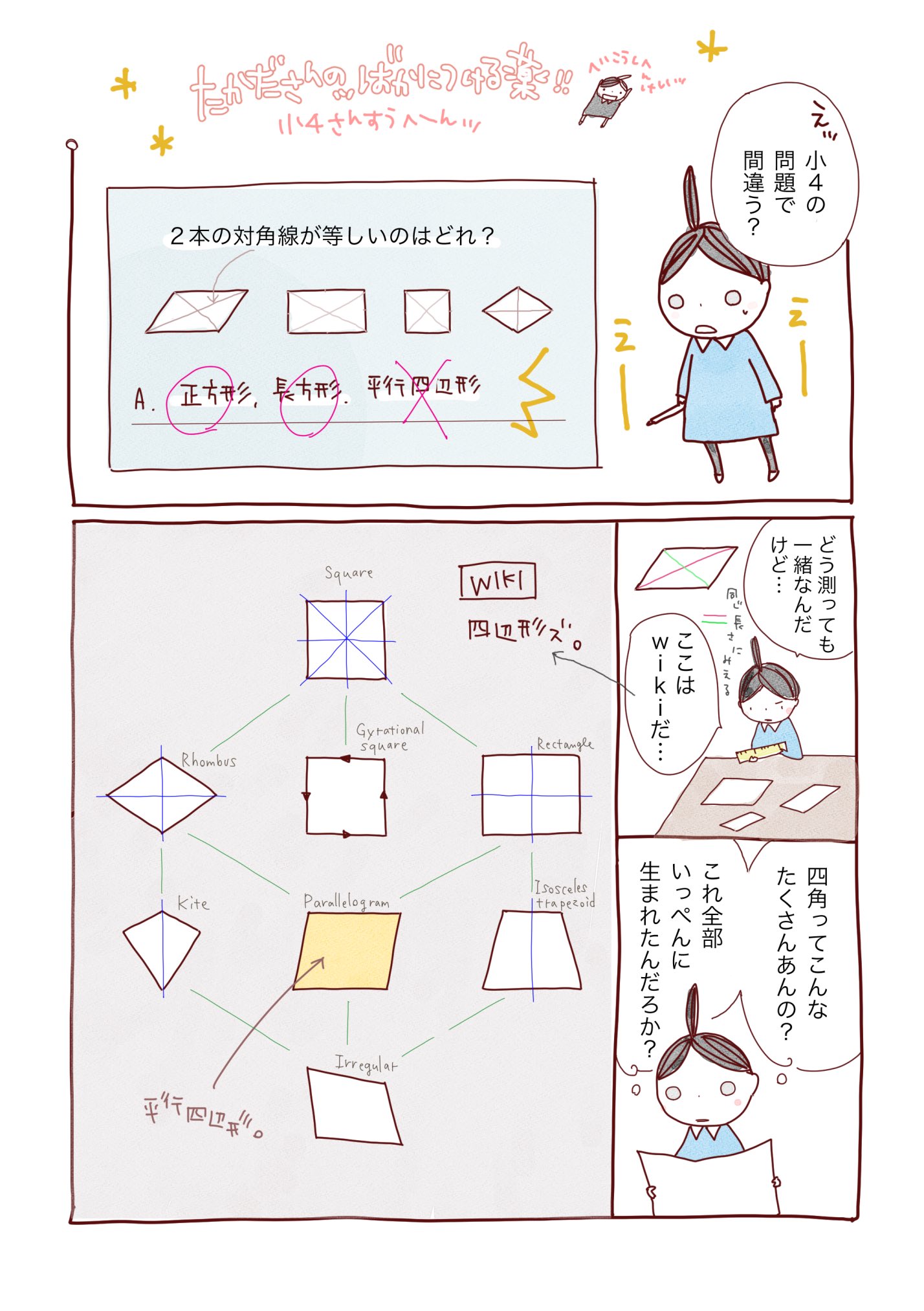平行四辺形であることを証明する 苦手な数学を簡単に
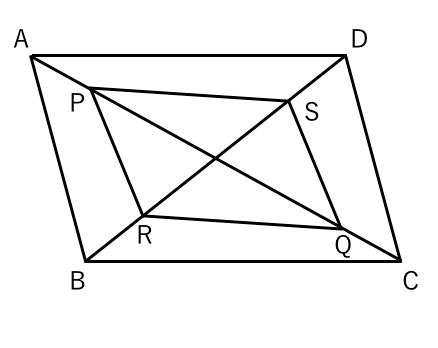
平行四辺形であることを証明する 苦手な数学を簡単に	平行四辺形であることを証明する 苦手な数学を簡単に	平行四辺形であることを証明する 苦手な数学を簡単に
平行四辺形であることを証明する 苦手な数学を簡単に	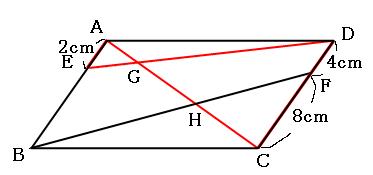平行四辺形であることを証明する 苦手な数学を簡単に	平行四辺形であることを証明する 苦手な数学を簡単に
平行四辺形であることを証明する 苦手な数学を簡単に	平行四辺形であることを証明する 苦手な数学を簡単に	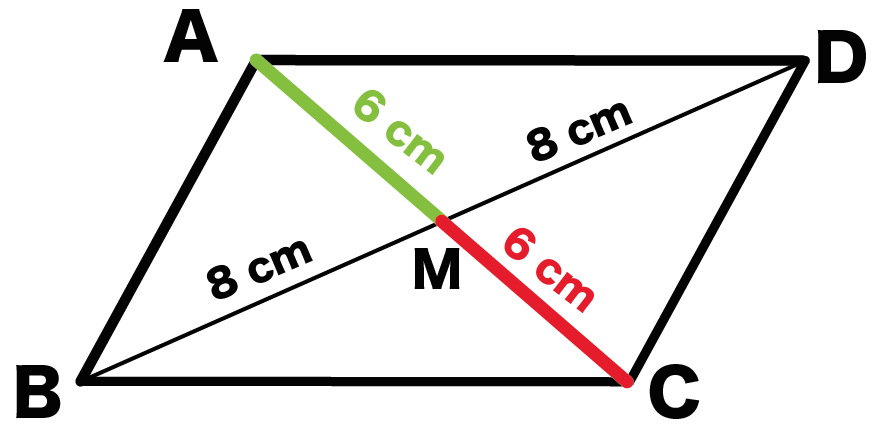平行四辺形であることを証明する 苦手な数学を簡単に
平行四辺形であることを証明する 苦手な数学を簡単に	平行四辺形であることを証明する 苦手な数学を簡単に	平行四辺形であることを証明する 苦手な数学を簡単に
平行四辺形であることを証明する 苦手な数学を簡単に	平行四辺形であることを証明する 苦手な数学を簡単に	平行四辺形であることを証明する 苦手な数学を簡単に
平行四辺形であることを証明する 苦手な数学を簡単に	平行四辺形であることを証明する 苦手な数学を簡単に	平行四辺形であることを証明する 苦手な数学を簡単に
平行四辺形であることを証明する 苦手な数学を簡単に	平行四辺形であることを証明する 苦手な数学を簡単に	平行四辺形であることを証明する 苦手な数学を簡単に
平行四辺形であることを証明する 苦手な数学を簡単に	平行四辺形であることを証明する 苦手な数学を簡単に	平行四辺形であることを証明する 苦手な数学を簡単に
平行四辺形であることを証明する 苦手な数学を簡単に	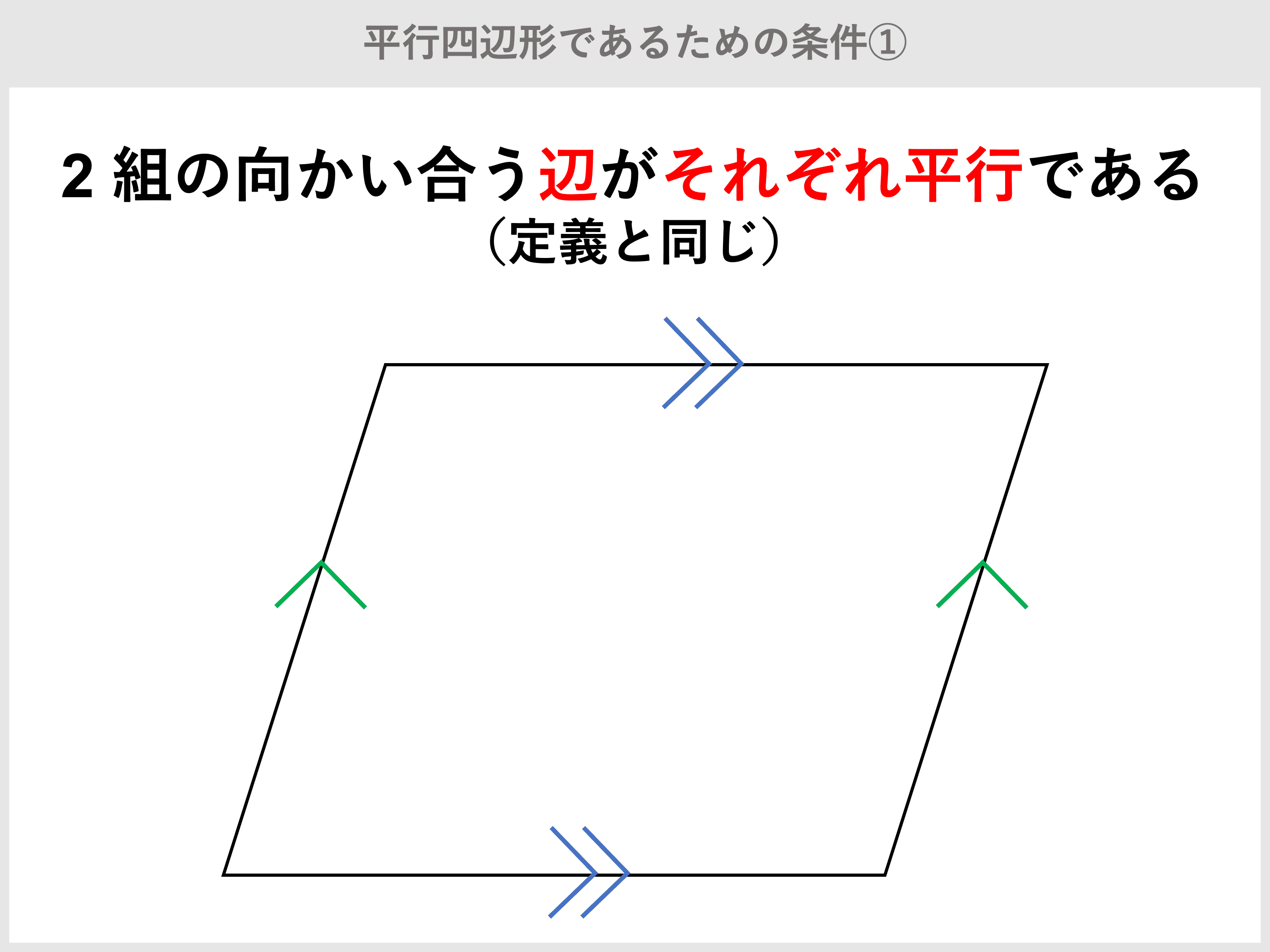平行四辺形であることを証明する 苦手な数学を簡単に	平行四辺形であることを証明する 苦手な数学を簡単に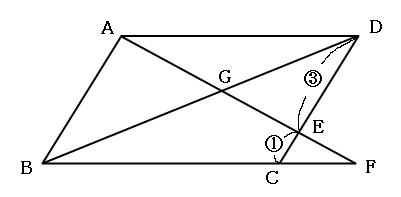
平行四辺形であることを証明する 苦手な数学を簡単に	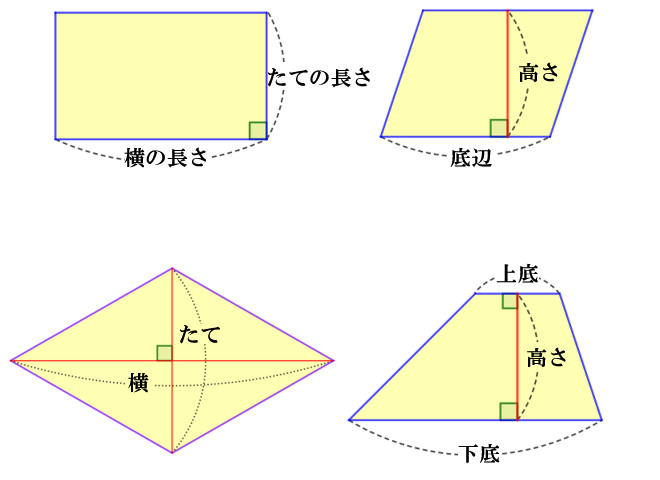平行四辺形であることを証明する 苦手な数学を簡単に	平行四辺形であることを証明する 苦手な数学を簡単に
平行四辺形であることを証明する 苦手な数学を簡単に	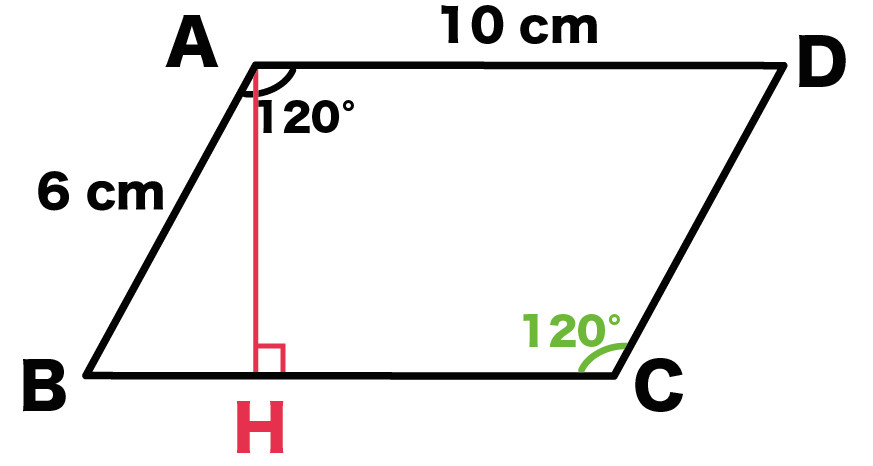平行四辺形であることを証明する 苦手な数学を簡単に	平行四辺形であることを証明する 苦手な数学を簡単に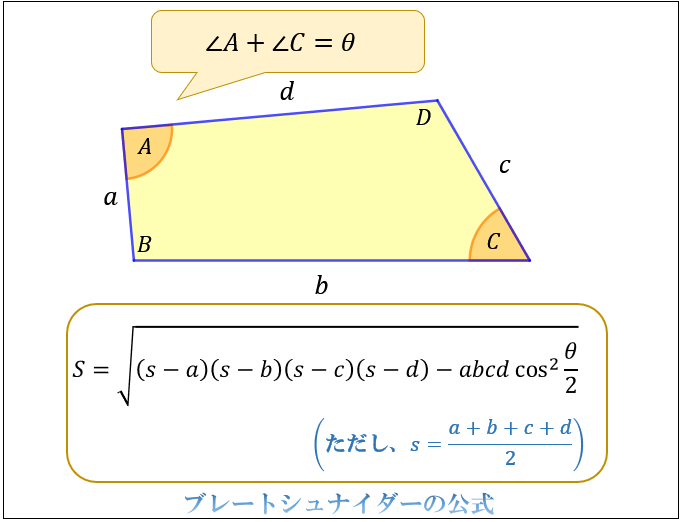
平行四辺形であることを証明する 苦手な数学を簡単に	平行四辺形であることを証明する 苦手な数学を簡単に	平行四辺形であることを証明する 苦手な数学を簡単に
平行四辺形であることを証明する 苦手な数学を簡単に	平行四辺形であることを証明する 苦手な数学を簡単に	平行四辺形であることを証明する 苦手な数学を簡単に
平行四辺形であることを証明する 苦手な数学を簡単に	平行四辺形であることを証明する 苦手な数学を簡単に	平行四辺形であることを証明する 苦手な数学を簡単に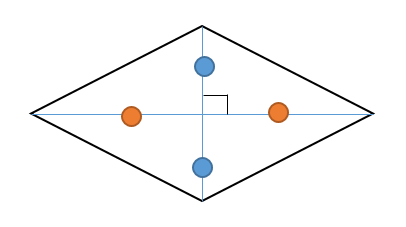
平行四辺形であることを証明する 苦手な数学を簡単に	平行四辺形であることを証明する 苦手な数学を簡単に	平行四辺形であることを証明する 苦手な数学を簡単に
平行四辺形であることを証明する 苦手な数学を簡単に	平行四辺形であることを証明する 苦手な数学を簡単に	平行四辺形であることを証明する 苦手な数学を簡単に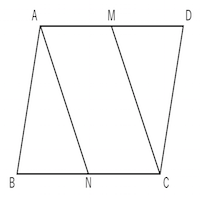
平行四辺形であることを証明する 苦手な数学を簡単に	平行四辺形であることを証明する 苦手な数学を簡単に	平行四辺形であることを証明する 苦手な数学を簡単に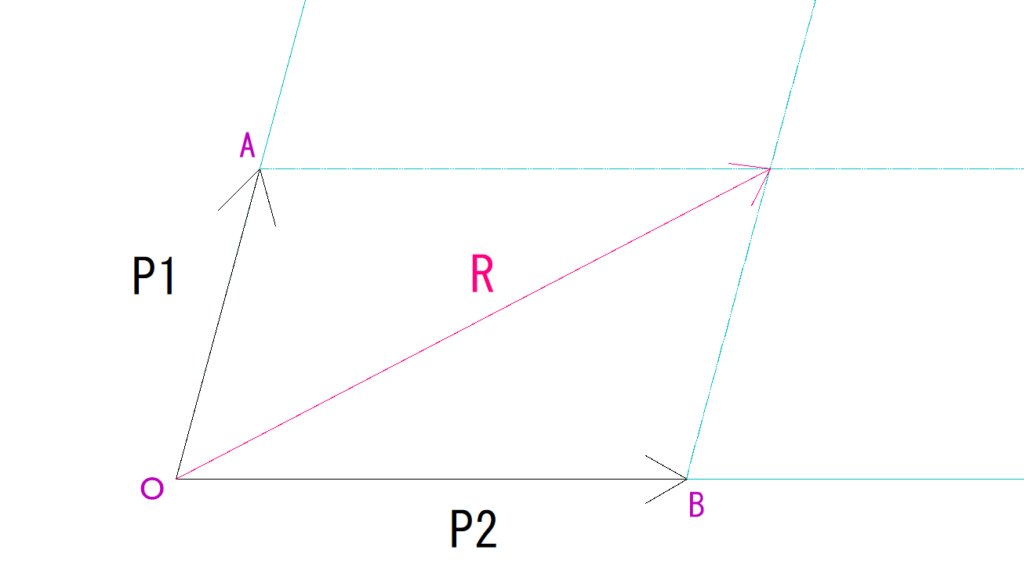
平行四辺形であることを証明する 苦手な数学を簡単に	平行四辺形であることを証明する 苦手な数学を簡単に	平行四辺形であることを証明する 苦手な数学を簡単に
平行四辺形であることを証明する 苦手な数学を簡単に	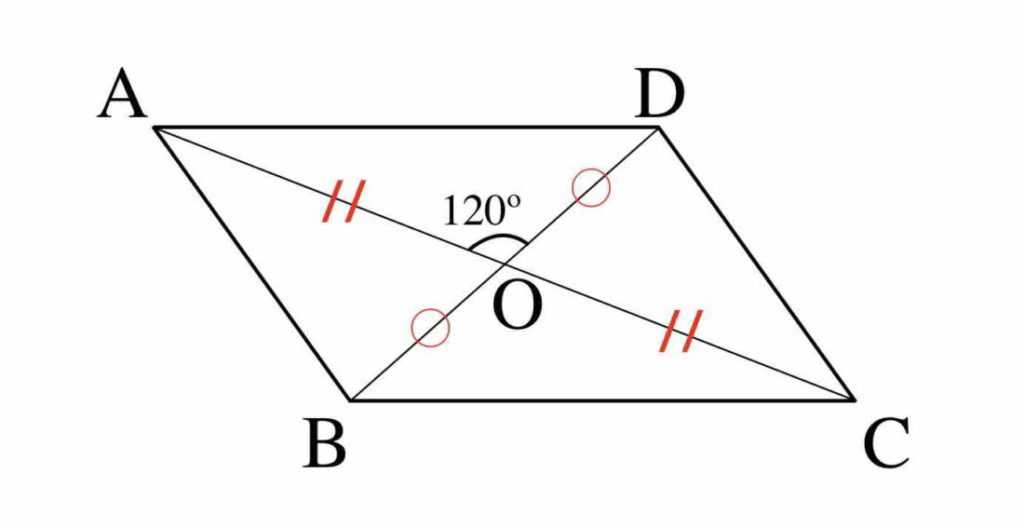平行四辺形であることを証明する 苦手な数学を簡単に	平行四辺形であることを証明する 苦手な数学を簡単に
平行四辺形であることを証明する 苦手な数学を簡単に	平行四辺形であることを証明する 苦手な数学を簡単に	平行四辺形であることを証明する 苦手な数学を簡単に
平行四辺形であることを証明する 苦手な数学を簡単に	平行四辺形であることを証明する 苦手な数学を簡単に	平行四辺形であることを証明する 苦手な数学を簡単に
平行四辺形であることを証明する 苦手な数学を簡単に	平行四辺形であることを証明する 苦手な数学を簡単に	平行四辺形であることを証明する 苦手な数学を簡単に
平行四辺形であることを証明する 苦手な数学を簡単に	平行四辺形であることを証明する 苦手な数学を簡単に	平行四辺形であることを証明する 苦手な数学を簡単に
平行四辺形であることを証明する 苦手な数学を簡単に	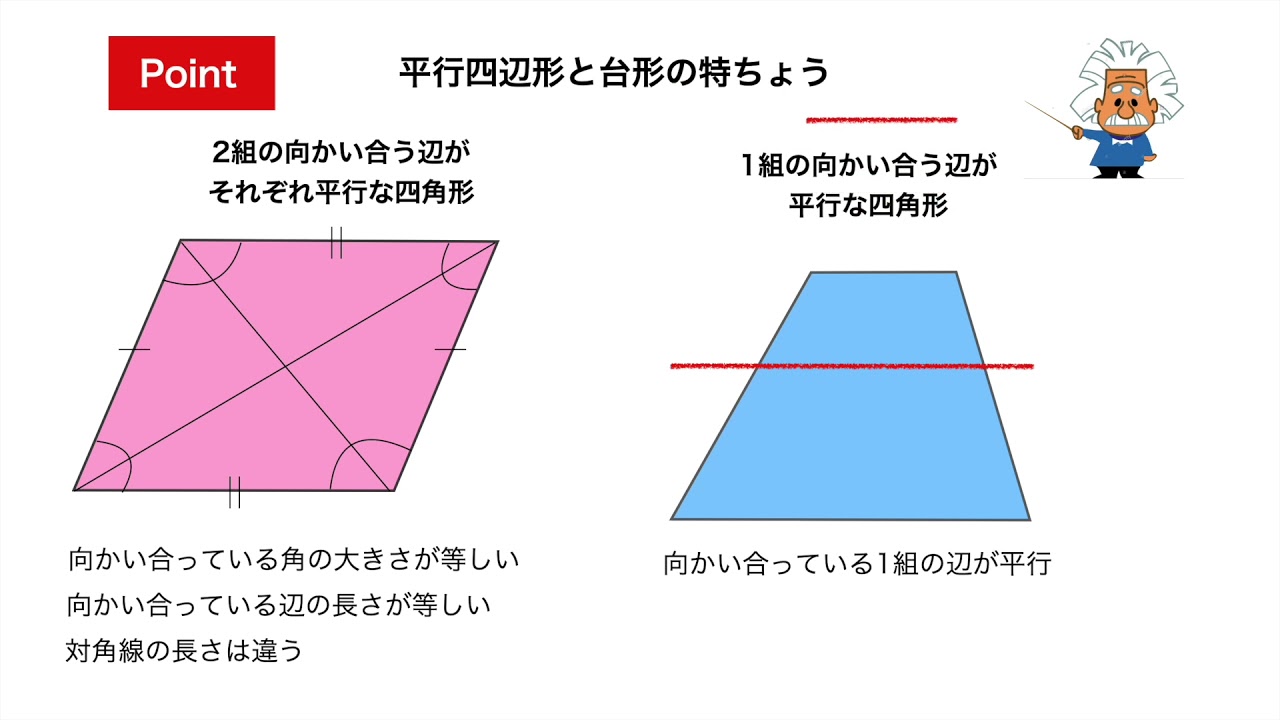平行四辺形であることを証明する 苦手な数学を簡単に	平行四辺形であることを証明する 苦手な数学を簡単に
平行四辺形であることを証明する 苦手な数学を簡単に	平行四辺形であることを証明する 苦手な数学を簡単に	平行四辺形であることを証明する 苦手な数学を簡単に
平行四辺形であることを証明する 苦手な数学を簡単に	平行四辺形であることを証明する 苦手な数学を簡単に	平行四辺形であることを証明する 苦手な数学を簡単に
平行四辺形であることを証明する 苦手な数学を簡単に	平行四辺形であることを証明する 苦手な数学を簡単に	平行四辺形であることを証明する 苦手な数学を簡単に
平行四辺形であることを証明する 苦手な数学を簡単に	平行四辺形であることを証明する 苦手な数学を簡単に	平行四辺形であることを証明する 苦手な数学を簡単に
平行四辺形であることを証明する 苦手な数学を簡単に	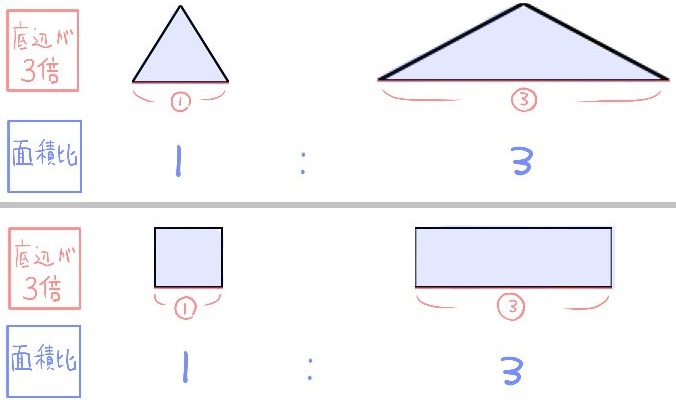平行四辺形であることを証明する 苦手な数学を簡単に	平行四辺形であることを証明する 苦手な数学を簡単に
平行四辺形であることを証明する 苦手な数学を簡単に	平行四辺形であることを証明する 苦手な数学を簡単に	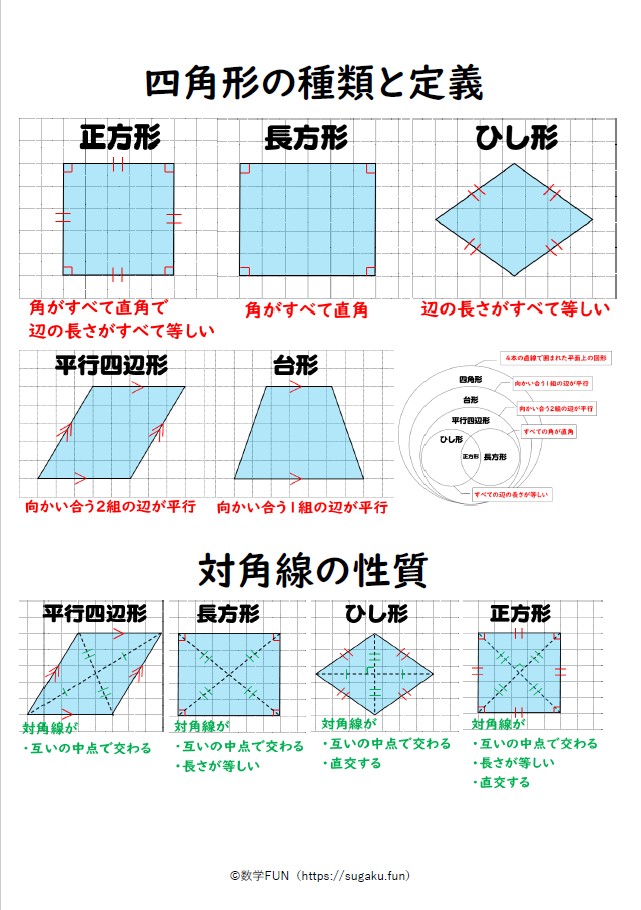平行四辺形であることを証明する 苦手な数学を簡単に
平行四辺形であることを証明する 苦手な数学を簡単に	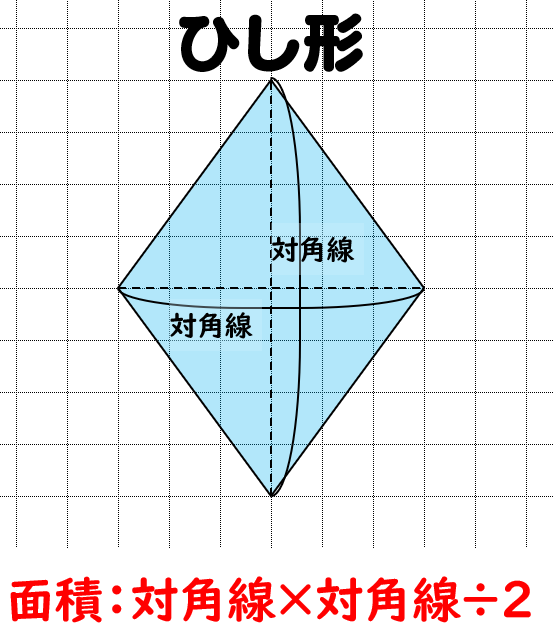平行四辺形であることを証明する 苦手な数学を簡単に	平行四辺形であることを証明する 苦手な数学を簡単に
平行四辺形であることを証明する 苦手な数学を簡単に	平行四辺形であることを証明する 苦手な数学を簡単に

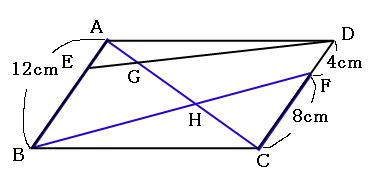
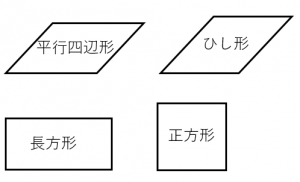
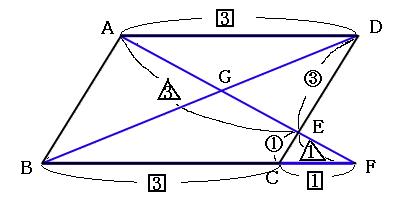
問題の見方 長方形，ひし形，正方形を別々に覚えるのではなく，すべて 平行四辺形の進化系 という視点でとらえましょう。 まず，四角形ABCDは平行四辺形なので，対辺，対角は等しくなります。 これに加えて，①はAB=BCより隣り合う辺が等しくなりますね。 つまり 辺が進化 して4辺が等しくなるので，ひし形ですね。 ②のAC=BDは 対角線が等しい ことを表している1分でわかる定義、正方形、平行四辺形との違い、対角線との関係 二等辺三角形の面積は？1分でわかる計算、公式、角度、高さがわからない場合の計算 100円から読める！ネット不要！印刷しても読みやすいpdf記事はこちら⇒ いつでもどこでも読める！広告無し！建築学生が学ぶ構造力学のpdf

Incoming Term: 平行四辺形 対角線 長さ 違う,